Desvio padrão é um conceito muito utilizado em ciência de dados. É uma base fundamental para qualquer cálculo estatístico. Nesse artigo, vamos mergulhar em um dos conceitos mais importantes (e às vezes mal compreendido) da análise de dados: desvio padrão.
O que é Desvio Padrão?
O desvio padrão é uma medida que nos diz quanto os dados estão "espalhados" em relação à média. Em outras palavras, ele mede a variabilidade dos seus dados. É perfeito para entender:
- Se as vendas mensais são consistentes ou muito variáveis
- O quanto os tempos de resposta de um site oscilam
- Se os salários de uma empresa são homogêneos ou muito discrepantes
- A consistência de um processo de fabricação.
Por que o Desvio Padrão é Importante?
Vamos usar um exemplo pra explicar melhor. Imagine dois vendedores:
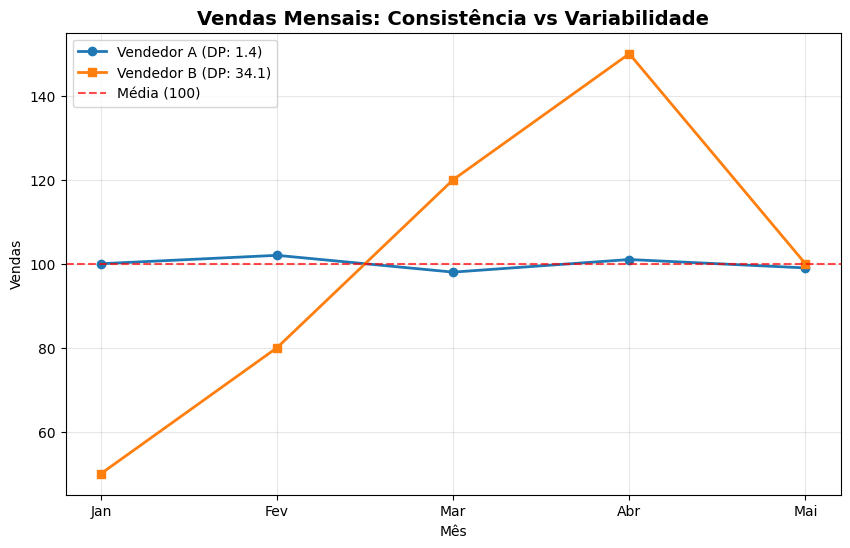
Vendedor A: Vendas mensais de [100, 103, 98, 101, 99] - média: 100. Já o vendedor B, tem as seguintes vendas mensais [50, 80, 120, 150, 100], cuja a média também é 100.
Ambos com a mesma média, mas qual você contrataria? O vendedor A é muito mais consistente do que o B. O desvio padrão ajuda a enxergar essas diferenças.
Vamos trabalhar com código?
Ferramentas Necessárias
Todas as vezes que vamos fazer algum projeto de estatística, a minha recomendação é sempre Jupyter Notebook. Essa ferramenta é fácil de usar e é feita para estatísticas e análise de dados.
Você pode usar outras ferramentas também, como Google Colab, que já vem tudo configurado, ou qualquer outra ferramenta que você queira.
Instalando as Bibliotecas
Antes de começar, você vai precisar instalar os pacotes necessários, caso não tenha. Você pode instalar diretamente do Jupyter. Basta abrir uma célula e rodar o seguinte comando:
%pip install pandas numpy matplotlib
Observe que mandei instalar vários pacotes (pandas, numpy e matplotlib) em uma linha. Roda a célula, usando Ctrl + Enter, ou simplesmente aperte o ▶. Aguarde o resultado e vamos partir para outra.
Quando tudo estiver instalado, vamos importar esses pacotes.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
Criando os Dados
Como estamos aprendendo, vamos começar com exemplos práticos. Eu vou criar alguns conjuntos de dados para você ver na prática a diferença que o desvio padrão faz. Vamos começar com os nossos vendedores:
vendedor_a = [100, 102, 98, 101, 99]
vendedor_b = [50, 80, 120, 150, 100]
Corre a célula. E vamos analisar essas vendas.
Calculando o Desvio Padrão - Metodo Manual
Antes de usarmos a função pronta, vamos entender no manual como funciona.
# Vendedor A
media_a = sum(vendedor_a) / len(vendedor_a)
print(f"Média Vendedor A: {media_a}")
# Calculando as diferenças da média
diferencas_a = [(x - media_a)**2 for x in vendedor_a]
print(f"Diferenças ao quadrado: {diferencas_a}")
# Desvio padrão (populacional)
desvio_a = (sum(diferencas_a) / len(diferencas_a)) ** 0.5
print(f"Desvio Padrão Vendedor A: {desvio_a:.2f}")
Deixa eu explicar o que fizemos:
- Calculamos a média: Somamos tudo e dividimos pela quantidade
- Calculamos as diferenças: Para cada valor, subtraímos a média
- Elevamos ao quadrado: Para eliminar valores negativos
- Tiramos a média das diferenças: Somamos e dividimos pela quantidade
- Tiramos a raiz quadrada: Para voltar à unidade original
Calculando com Numpy (Método Fácil)
O Python faz tudo mais fácil. Tudo isso que fizemos tem uma função pronta. Vamos usá-la:
# Usando NumPy para calcular
desvio_a_numpy = np.std(vendedor_a)
desvio_b_numpy = np.std(vendedor_b)
print(f"Desvio Padrão Vendedor A: {desvio_a_numpy:.2f}")
print(f"Desvio Padrão Vendedor B: {desvio_b_numpy:.2f}")
print(f"\nO Vendedor B tem {desvio_b_numpy/desvio_a_numpy:.1f}x mais variabilidade!")
Você vai observar que o vendedor B tem uma variedade muito maior.
Mas, só estamos nos números. Vamos visualizar essa diferença.
Visualizando a Diferença
# Criando o gráfico
plt.figure(figsize=(10, 6))
# Plotando os dois vendedores
meses = ['Jan', 'Fev', 'Mar', 'Abr', 'Mai']
plt.plot(meses, vendedor_a, marker='o', label=f'Vendedor A (DP: {desvio_a_numpy:.1f})', linewidth=2)
plt.plot(meses, vendedor_b, marker='s', label=f'Vendedor B (DP: {desvio_b_numpy:.1f})', linewidth=2)
# Adicionando linha da média
plt.axhline(y=100, color='red', linestyle='--', alpha=0.7, label='Média (100)')
plt.title('Vendas Mensais: Consistência vs Variabilidade', fontsize=14, fontweight='bold')
plt.xlabel('Mês')
plt.ylabel('Vendas')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
Desvio Padrão Populacional vs Amostral
Existe uma diferença importante entre esses dois e você precisa saber. A diferença principal são os dados que você tem em mãos.
O desvio padrão populacional é quando você tem todos os dados da população. No caso, você usa N no denominador para quantidade total. Por exemplo, quando você tem todas as vendas de todos os vendedores em um grupo de 50 vendedores.
O desvio padrão amostral é quando você tem apenas uma amostra dos dados. Nesse caso, você vai usar N-1 no denominador. Por exemplo, se você tivesse as vendas somente de 30 dos seus vendedores, isso seria amostral.
Como isso seria calculado?
# Desvio padrão populacional (ddof=0) - quando você tem TODOS os dados
dp_populacional = np.std(vendedor_a, ddof=0)
# Desvio padrão amostral (ddof=1) - quando você tem uma AMOSTRA
dp_amostral = np.std(vendedor_a, ddof=1)
print(f"Desvio Populacional: {dp_populacional:.3f}")
print(f"Desvio Amostral: {dp_amostral:.3f}")
print(f"Diferença: {dp_amostral - dp_populacional:.3f}")

Conclusão
O desvio padrão é uma das métricas mais importantes da ciência de dados. Ele nos ajuda a entender não apenas "onde estão" nossos dados (média), mas também "quão espalhados" eles estão.
Em poucos minutos você aprendeu os conceito básico de desvio padrão. Agora, é só praticar com seus próprios dados!
Lembre-se: dados com mesma média podem ter comportamentos completamente diferentes. O desvio padrão é quem vai te contar essa história.
Se você curtiu esse conteúdo, compartilhe com alguém que também está aprendendo estatística aplicada!

Comentários (0)
Seja o primeiro a comentar!
Deixe um comentário