A regressão linear simples é a porta de entrada para o universo dos modelos de aprendizado supervisionado, ou machine learning. Neste post, vamos falar tudo sobre esse método simples, mas extremamente poderoso.
Apesar de parecer básico, a regressão linear simples serve como base para técnicas muito mais sofisticadas. Ela é fundamental para entender relações lineares entre uma variável explicativa (geralmente chamada de X) e uma variável-alvo (y).
Vamos entender mais sobre essa ferramenta importantíssima.
O que é Regressão Linear Simples?
A regressão linear simples é um modelo matemático que busca representar a relação entre duas variáveis: uma independente (X) e uma dependente (y). A variável X é também considerada explanatória. Mas a ideia é prever o valor da variável dependente com base nos valores da variável independente.
Em outras palavras, o modelo tenta "desenhar" uma linha reta que melhor se ajusta aos dados disponíveis — uma linha que resume a tendência entre essas duas variáveis. Essa linha é definida por uma equação do tipo:
y = a + bX
Onde:
- y é o valor que queremos prever (variável dependente),
- X é a variável independente,
- a é o intercepto (onde a linha cruza o eixo y),
- b é o coeficiente angular (a inclinação da linha, que mostra o quanto y muda quando X muda).
Importante
Nem todos os dados vão ser relativos entre as variáveis. Por exemplo, altura e idade. A idade não tem nada a ver com a altura do indivíduo. Claro que quanto mais velho a pessoa se torna, naturalmente, ela vai encolhendo. Em contra partida, a mudança de altura é inexistente quando observado entre idades de 20 a 30 anos. Isso quer dizer que a idade não causa a mudança de altura.
Agora, se formos observar as horas que um estudante gasta estudando, e comparar com a nota recebida, vamos ver que as horas (X) diretamente modificam a variável dependente (y).
Regressão Linear
Uma coisa muito importante no assunto de regressão linear é o fato de que não existe uma garantia de relacionamento. Então, antes de tentar usar, temos que analisar se um relacionamento existe. Vamos dar uma analisada nisso.
Relacionamento Claro
Para demostrar como funciona um relacionamento claro, vou usar uma dataframe que já existe e só precisamos puxar do pacote. Para isso vamos ter que importar alguns pacotes.
Lembre-se que se não tiver algum desses pacotes, simplesmente passe um pip install
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.api as sm
Assim que tiver tudo importado, vamos agora passar o comando para puxar os dados
# Carregar dataset
tips = sns.load_dataset("tips")
Com isso temos os nossos dados. Agora eu quero selecionar as duas colunas com que vou trabalhar.
Quando você senta para comer em um restaurante nos Estados Unidos, na maioria das vezes, a gorjeta não é parte da conta. O valor fica a critério do consumidor. Contudo, há expectativas. Gorjetas devem ser pelo menos 15% da conta. Nem sempre as pessoas seguem isso.
A minha hipótese é que o valor da gorjeta está diretamente relacionada ao valor da conta. Então vamos examinar o total_bill (o valor total da conta) e o tip (gorgeta).
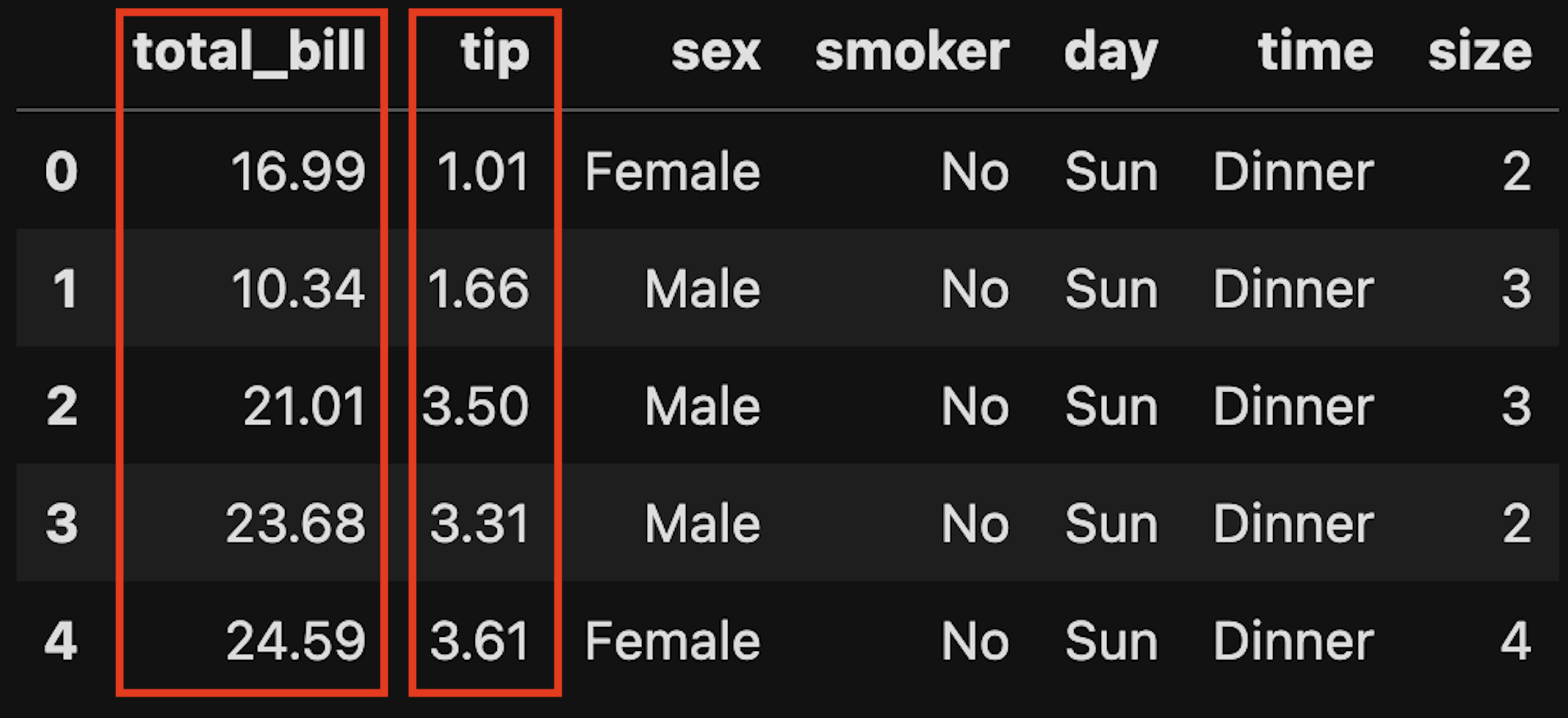
Vamos analisar com mais profundeza. O total_bill é a variável independente (X). Pois se a gorjeta é 15% da conta, então o valor do tip vai depender completamente do valor total da conta. Vamos definir as variáveis.
# Definir variáveis
X = tips["total_bill"]
y = tips["tip"]
Determinamos o X e o y. Agora vamos adicionar o intercepto.
# Adicionar constante para o modelo
X_const = sm.add_constant(X)
Por que estamos adicionando essa função? Isso cria uma coluna extra que representa o intercepto. Por padrão, em uma regressão linear simples, o intercepto entre o X e y é no zero. Mas isso não representa os dados necessariamente.
Por exemplo, o gráfico abaixo mostra como o padrão (linha pontilhada vermelha) não se alinha com os dados. Agora já a linha azul com a constante, mostra alinhamento com os dados reais.
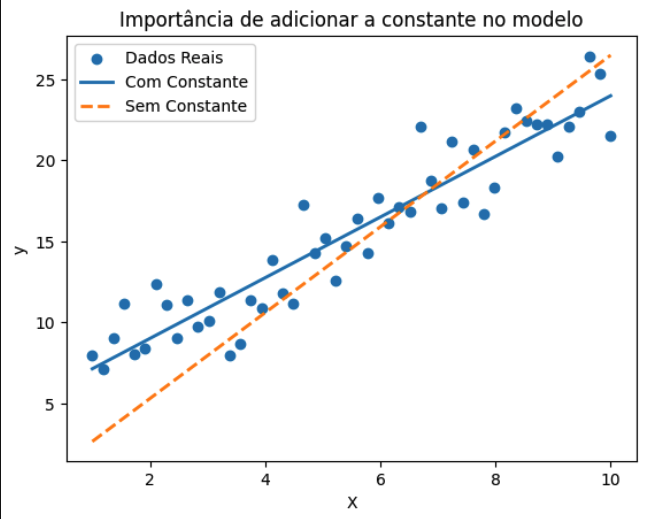
De volta ao nosso assunto: vamos falar sobre o resumo do modelo.
# Ajustar modelo de regressão linear
model = sm.OLS(y, X_const).fit()
print(model.summary())
Resumindo o Modelo
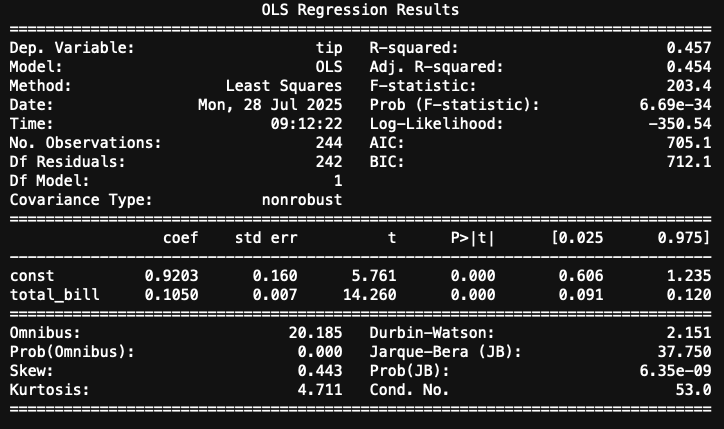
A imagem acima mostra o resumo do modelo. O que tudo isso significa?
Vamos resumir as coisas mais importantes nisso tudo.
O valor do R² (R-squared) foi de 0.457, o que significa que cerca de 45,7% da variação no valor da gorjeta pode ser explicada pelo valor da conta. Em outras palavras, quase metade da variação nos valores das gorjetas é explicada pelo tamanho da conta. Para um modelo simples, esse é um resultado considerado razoavelmente bom, já que estamos usando apenas uma variável preditora.
O F-statistic foi 203,4 com um p-valor praticamente zero (6.69e-34). Isso indica que o modelo, como um todo, é estatisticamente significativo. Ou seja, existe evidência suficiente para afirmar que a variável explicativa (total_bill) tem de fato relação com a variável dependente (tip).
Interpretando os Coeficientes
A constante intercepto de 0.9203 mesmo que a conta fosse de zero reais, o modelo prevê uma gorjeta de aproximadamente 0,92. Na prática, funciona mais como um ponto de ajuste do modelo do que como um valor interpretável (afinal, ninguém paga conta zero).
O coeficiente de total_bill 0.1050 é o ponto central da análise. Para cada aumento de 1 na conta, a gorjeta aumenta em média de 0,105. Ou seja, se uma conta sobe R$ 10, espera-se que a gorjeta aumente cerca de R$ 1,05.
Quando Usar Regressão Linear Simples?
Nem sempre a regressão linear simples funciona. Em alguns casos, outros modelos são mais práticos. A primeira etapa é sempre analisar se faz sentido supor um relacionamento linear entre as variáveis. Por exemplo, usando os mesmos dados e analisando variáveis diferentes, vamos ver que nem sempre tem uma relação.
Usando as variáveis tips (gorjetas) como o X, e o day_num (dia da semana) como o y. Vamos ver que não existe relação para regressão linear simples. Isso não quer dizer que não dá para usar machine learning, mas que esse modelo não é o adequado.
tips["day_num"] = tips["day"].astype("category").cat.codes
X2 = tips["day_num"]
y2 = tips["tip"]
X2_const = sm.add_constant(X2)
model2 = sm.OLS(y2, X2_const).fit()
sns.regplot(x="day_num", y="tip", data=tips)
plt.title("Gorjeta por dia da semana (sem relação linear)")
plt.show()
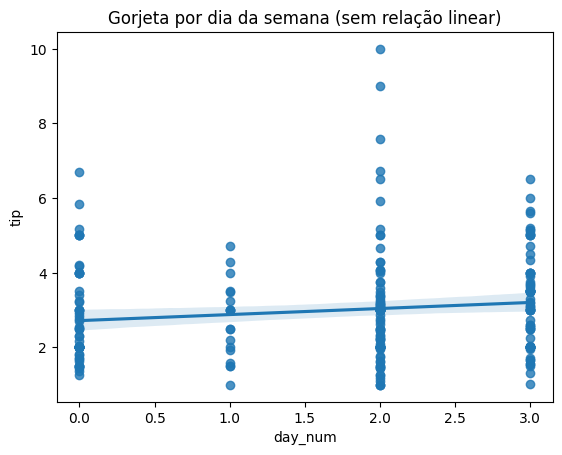
Quando houver um padrão, como no exemplo da conta e da gorjeta, a regressão linear simples se torna uma ferramenta poderosa. Ela permite quantificar a relação: entender quanto a variável dependente (y) deve mudar quando a variável independente (X) aumenta em uma unidade. Esse tipo de análise é útil em diversas áreas, desde negócios (por exemplo, prever vendas com base em investimentos em marketing), até saúde (como relacionar horas de sono com desempenho cognitivo).
Outro ponto fundamental é não esquecer do intercepto, usando o sm.add_constant(X). Como vimos, forçar a linha a passar pela origem pode distorcer completamente o modelo. Na prática, isso significa perder a capacidade de representar adequadamente os dados reais.
Por fim, é importante lembrar que a regressão linear simples é apenas a porta de entrada. A partir dela, podemos avançar para modelos mais complexos, como a regressão múltipla (com várias variáveis independentes), modelos não lineares e até algoritmos de machine learning mais sofisticados. Mas, sem compreender bem a base — que é a regressão linear simples —, fica muito mais difícil dar os próximos passos.
Conclusão
A regressão linear simples pode parecer apenas uma equação com duas letras, mas ela é muito mais do que isso. É uma ferramenta poderosa para explorar, entender e prever comportamentos em dados. Ao dominar esse conceito, você estará mais preparado para enfrentar modelos mais complexos no universo do machine learning.

Comentários (0)
Seja o primeiro a comentar!
Deixe um comentário